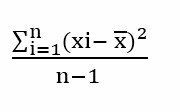The brīvības pakāpes Mūsdienu statistikā tie veido centrālo saturu, tomēr to definīcija ir ļoti neskaidri izskaidrota grāmatās par šo tēmu.
Tās jēdziens ir viegli saprotams no ģeometriskā, algebriskā un intuitīvā viedokļa.
Sludinājumi
Ģeometrija nosaka brīvības pakāpes kā atstarpes, pēc kurām kopsavilkuma mērvienība var mainīties un parādīt dažādas vērtības. No algebriskā viedokļa to saprot kā vienādojumu skaitu, kas izveidots, izmantojot datus.
Abas definīcijas ir saistītas ar palīdzību jēdziena izpratnē, jo tā pielietojums ir izplatīts visā statistikas zinātnē.
Sludinājumi
Šajā rakstā jūs atradīsit:
Kas ir pazīstams kā brīvības pakāpes?
Lai nedaudz vairāk saprastu šo tēmu, zemāk es sniedzu dažas definīcijas, kas atrodamas bieži lietotajos statistikas tekstos:

Sludinājumi
Brīvības pakāpju definīcijas
Pēc Daniela Veina teiktā: "Tā ir vērtību, noviržu un individuālo vērtību summa attiecībā pret to vidējo vērtību, kas vienāda ar nulli" n-1 vērtības no vidējā, n-tā vērtība ir zināma, automātiski noteikta ar 3 ierobežojumu, kur visas n vērtības summējas nulle.
Dawsonam "Brīvības pakāpes un to vērtība ir saistītas ar iespēju skaitu, kurās tiek izmantota informācijas parauga."
Sludinājumi
Visbeidzot, bet ne mazāk svarīgi Pagano saprot “Brīvības pakāpes kā tādu datu skaitu, kuriem nav izmaiņu, aprēķinot statistisko testu”.
Kādas ir brīvības pakāpes?
The GL (brīvības pakāpes) ir informācijas sniegtais datu daudzums, ko var izmantot, lai novērtētu nezināmos populācijas parametrus un aprēķinātu tāmes mainīgumu.
Sludinājumi
To nosaka pēc modeļa parametru skaita un modeļa novērojumiem šovs. Palielinoties izlases lielumam, tiek iegūta vairāk informācijas un attiecīgi palielinās datu brīvības pakāpes. Gadījumā, ja modelim tiek pievienoti parametri, piemēram, regresijas vienādojuma termini tiek palielināti, izdevumu informācijas samazināšana un iespējamās brīvības pakāpes samazināšana, lai novērtētu VVP vērtējumu mainīgumu parametriem.
Tos izmanto arī, lai definētu noteiktu sadalījumu, sadalījumu saimes, piemēram, F, t, chi-kvadrāts, to izmanto GL, lai modelī norādītu atbilstošu specifisko sadalījumu dažādiem izlases lielumiem un dažādiem parametru apjomiem.
Noslēgumā, brīvības pakāpes GL attiecas uz statistikas aprēķinos nepieciešamo neatkarīgo vērtību skaitu, atskaitot novērojumiem pievienoto ierobežojumu skaitu. Tas ir, pēc vērtību uzzināšanas par minēto paraugu var brīvi norādīt vērtību skaitu izlasē.
Brīvības pakāpju izmantošana
The brīvības pakāpes tie obligāti ir saistīti ar izlases lielumu, tāpēc tos izmanto statistisko sadalījumu definīcijā, lai veiktu hipotēzes testus.
Tos izmanto, aprēķinot standarta novirze parauga izkliedes pakāpi attēlojot ar n datiem ap vidējo un Zinot vidējo, attiecības starp datiem tiek noteiktas, tos saskaitot un dalot ar to skaitu. paši.
Tie ir pamats Studenta t sadalījumam, kas tiek izmantots, lai pārbaudītu hipotēzes par vidējo vienlīdzību starp divām datu grupām.
Tās izmantošana galvenokārt tiek diferencēta starp statistiku, kas tiek izmantota populācijas parametri Jā parādi viņiem.
Populācijas parametros, ņemot vērā, ka n ir zināmas visas vērtības, brīvības pakāpes būs visi iedzīvotāju elementi "N ".
Parauga parametriem tie ir aprēķini, jo visas izlases vērtības ir zināmas.
Abi gadījumi ļauj izlases kopas novērojumiem būt nejaušiem, tāpēc, novērtējot statistiku, jūs varat iegūt atšķirīgus rezultātus. Tātad novērojumiem ir dažādas īpašības, piemēram, iedzīvotāju kopas novērojumi.
Izpratne par brīvības pakāpēm
Lai labāk izprastu brīvības pakāpju skaits, ieteicams to redzēt kā izmēru skaitu telpā, kurā vērtība var brīvi mainīties vai pārvietoties.
Katra saikne tiek izveidota vai aprēķināta pēc pašas izlases sniegtajiem datiem, kas rada nepieciešamību modificēt brīvības pakāpes GL, ja aprēķinos tiks izmantota statistika nākotnes līgumi. Šajā ziņā, brīvības pakāpes tie paliek ierobežoti ar starpību, kas rodas datu apjoma un starp tiem izveidoto attiecību apjoma dēļ.
Tos var aprēķināt pēc formulas:
N - r
Kur n ir vienāds ar paraugam piederošo subjektu skaitu, kas var pārspēt vērtību.
Kur r ir vienāds ar subjektu skaitu, kuru vērtība būs atkarīga no izlases brīvo elementu vērtības.
Visbeidzot, ir vērts pieminēt, ka, tāpat kā citas tēmas statistikā, brīvības pakāpes statistikā viņiem ir svarīga loma citu jomu, piemēram, zinātnes un sabiedrības, pētījumos.