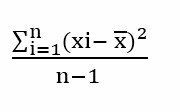Değişken, algoritmalarda, formüllerde ve matematiksel işlevlerde görünen ve farklı değerler alabilen bir semboldür. Belirli özelliklerine göre farklı şekillerde sınıflandırılırlar.
Değişkenler diğerleri arasında rastgele, sürekli, bağımlı, bağımsız, nicel, nitel olabilir. Bu sefer tanıyacağız ayrık değişkenler.
Reklamlar
Bu yazıda şunları bulacaksınız:
Ayrık değişkenin tanımı

Ayrık bir değişken şu şekilde bilinir: değerleri kabul etmenin koşullarını sunar belirli bir sayısal kümenin yani herhangi bir değeri benimseyemez, sadece bir kümenin değerlerini alır.
Reklamlar
Bu ayrık değişkendeki gözlemlenebilir değerler arasında olası olmayan bir mesafe olduğuna dikkat edilmelidir. ara değerlerle tamamlanırsa, iki değer arasında en az bir değer olmayabilir gözlemlenebilir.
Başka bir deyişle, ayrık değişkenler, herhangi iki değer arasında kaydedilebilir sayıda değere sahip sayısal değişkenlerdir. Örneğin, kullanıcı şikayetlerinin sayısı, kayıtlı arızaların sayısı.
Reklamlar
Ayrık değişken örnekleri
Ayrık değişkenler her zaman nicel veya sayısaldır, örneğin:
- Bir ailedeki kadın sayısı.
- Sahip olduğumuz parmak sayısı.
- Bir futbol maçı sırasında meydana gelen faullerin sayısı.
- Bir klinikte acil servise başvuran kişi sayısı.
- Bir parktaki ağaç sayısı.
- Evde izleyebileceğiniz televizyon kanallarının sayısı.
- Bir şirketin çalışan sayısı.
- Amazon'da aylık satılan kitap sayısı.
- Günde bir süpermarketi ziyaret eden kişi sayısı.
Sürekli değişken ve ayrık değişken arasındaki fark
Bir boyutun miktarı, aynı boyuttaki başka bir miktar (birim) ile karşılaştırılarak belirlenir.
Reklamlar
Bir değişken, herhangi bir sonlu aralık arasında sonsuz değerlere ulaşırsa süreklidir. Aksine, herhangi bir sonlu aralık içinde yalnızca sonlu değerlere ulaşan bir değişken ayrıktır.
Sürekli bir miktar, ölçüm yöntemiyle belirlenir. Sürekli ölçüm yöntemi, bir miktarın birim miktardan daha büyük veya daha az olduğu zamanları saymaktan oluşur. Örnek: Bir hastanın ateşi termometre ile ölçülür ve belirli zamanlarda daha yüksek veya daha düşük olabilir. 37 ila 39.5 arasında değişebilir.
Reklamlar
Ayrık bir miktar numaralandırma ile belirlenir. Bu numaralandırma yöntemi, içerdiği birim miktarları saymaktan oluşur. Örnek: Bir futbol takımının ayrık büyüklüğü, sahip olduğu 11 oyuncu olan oyuncu birimlerinin sayılmasıyla belirlenir.
Kesintili bir değişkeni sürekli bir değişkenden ayıran temel bir özellik, sürekli değişkenin asla ölçülmemesidir. Ayrık bir değişkenin aynı doğruluğu ile gözlenen değer, ölçüm cihazının kesinliğine bağlı olacaktır. Kullanılmış. Bu nedenle, sürekli bir değişkeni ölçerken, kaçınılmaz olarak bir ölçüm hatası meydana gelebilir, örneğin: bir kişinin sıcaklığı 37.6, 37.8, 38 olabilir.
Bu ikisinin nicel değişkenler olarak bilinen bir grup değişkenin parçası olduğunu belirtmekte fayda var.
Ayrık olasılık dağılımı
Kesikli bir değişken için bir olasılık dağılımı, olası olasılıkların özel bir listesidir. sayısal sonuçlar, böylece belirli oluşma olasılığı her biri ile ilişkilendirilir Sonuç.
Rastgele ayrık değişkenin beklenen değeri, sonuçların ağırlıklı ortalaması olarak ortaya çıkıyor. olasıdır, burada ağırlıkların her biri, her bir sonuçla ilişkili olasılıklardan kaynaklanır.
Nerede:
Xi = i - ilgilenilen ayrık değişken olan X'in inci sonucu.
P (Xi) = X'in i-inci sonucunun oluşma olasılığı
i. terim, aynı terimlerin hesaplanma şeklini belirleyen kuralı temsil eder. n-eleman i-th mertebe istatistiği en küçük i-th elementtir. Minimum veya ilk sipariş.
Rastgele bir kesikli değişkenin (s 2) varyansı, olası sonuçlar ile bunların ortalamaları arasındaki farkların ağırlıklı ortalaması olarak belirtilir.
Rastgele değişken X, gerçek bir sayıyı örnek uzayın farklı noktalarıyla ilişkilendiren bir fonksiyondur.
Kesikli değişken, süreksiz değişken olarak da bilinir, önceden belirlenmiş değerlerin sonlu miktarlarının bir sonucunu üretir, bu da yolunu sonlu yapar.
Son olarak, ayrık bir X değişkeninin, x1, x2, x3, xn ile tanımlanmış bir dizi olası değere sahip olduğu söylenir. olasılıklar p1, p2, p3, pn., yani bir varyasyon alanı içinde yalnızca belirli değerlerin kabul edilmesine izin verilir. belirlenen.
Genel olarak, ayrı bir değişken bir örneğin sonuçlarını temsil eder, böylece P (X = x) ile X'in x değerine ulaşma olasılığını anlarız. Daha sonra bu değişkenin değerlerini göz önünde bulundurarak, rastgele X'in x'in farklı gerçekleşmelerine bir olasılık atayan matematiksel bir denklem geliştirmek mümkündür.
İstatistik bilimlerinde değişken, kabul edilebilecek çeşitli değerleri benimsemeye duyarlı bir şekilde dalgalanma olanağına sahip bir ölçüdür. Dikkat edin, bu değişkenlerin diğer değişkenlerle ilişkili olduklarında bir değer kazandıklarını, bazı hipotezlerin veya bazı hipotezlerin bir parçasını oluşturduğunu akılda tutmak önemlidir. teori.